
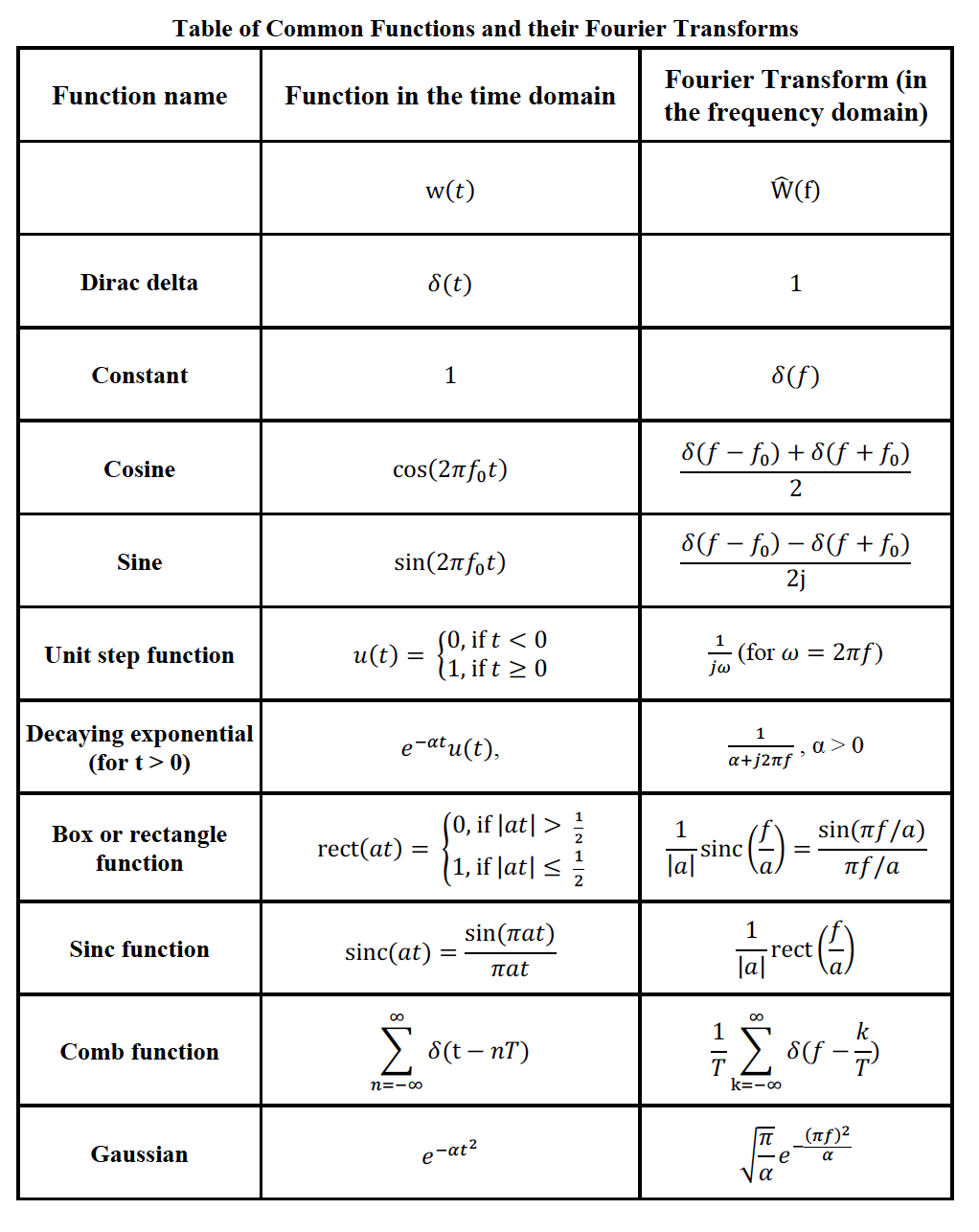
The derivation can be found by selecting the image or the text below. That is, we present several functions and there corresponding Fourier Transforms.

Under certain conditions the following inversion formulas for (A), (B), (C) hold: (A' ) f(x) = 2 J g (y)cos(xy)dy 11 0 c 2 J (B') f (x) gs(y)sin(xy)dy 11 0 -1 00 -ix (C' ) f(x) = (211) J ge(y)e Ydy In the following parts I, II, III tables for the transforms (A), (B) and (C) are given. This section gives a list of Fourier Transform pairs.

Take the Fourier Transform of both equations.
#FOURIER TRANSFORM TABLE PDF#
However, as you have access to this content, a full PDF is available via the Save. t 0 u(x 0) f(x) using Fourier Transforms. Table of Fourier Transform Pairs Function, f(t) Fourier Transform, F(w) Definition of Inverse Fourier Transform Definition of Fourier Transform 1 F (w ). similar tables of integral Fourier transforms the results are of mathematical and.
#FOURIER TRANSFORM TABLE SERIES#
If xT (T) is the periodic extension of x (t) then: Where cn are the Fourier Series coefficients of xT (t) and X () is the Fourier Transform of x (t) Furthermore. This means that g(y) for the remaining part of y cannot be given in a reasonably simple form. HTML view is not available for this content. Then (a) is called the discrete Fourier transform (DFT) of (ar). Relationship between Transform and Series. In some cases the result function g(y) is given over a partial range of y only. A possible analytic continuation to complex parameters y* should present no difficulties. The fast Fourier transformation1 (FFT) is widely used in many digital signal processing applications in both the frequency and time domain. The transform parameter y in (A) and (B) is assumed to be positive, while in (C) negative values are also included. Again, the follow- ing tables contain a collection of integrals of the form J f(x)cos(xy)dx Fourier Cosine Transform (Al o (B) J f(x)sin(xy)dx Fourier Sine Transform o (C) ge(y) = J f(x)eixYdx Exponential Fourier Transform -00 Clearly, (A) and (B) are special cases of (C) if f(x) is respec- tively an even or an odd function. So, in general, we can say that: If x(t) has Fourier transform X(), then X(t) has Fourier transform 2x( ). Known errors have been correc- ted, apart from the addition of a considerable number of new results, which involve almost exclusively higher functions. The Fourier transform and its inverse are symmetric X() Z 1 1 x(t)e jtdt x(t) 1 2 Z 1 1 X()ejtd except for the minus sign in the exponential, and the 2 factor.

All corresponding properties appear in a. similar tables of integral Fourier transforms the results are of mathematical and. This appendix provides a synthesis of the Fourier transform properties presented in Chapters 25 in a single table. Fourier transform theory is of central importance in a vast range of applications in physical science, engineering, and applied mathematics. Re > 0 21 Σ 2lt - nT,) 811 - 12) = S Seelikud - ¿ Cariken a + jw in 1)! (a + jo)" 21 ? + G(no)8(w - nah), 2.These tables represent a new, revised and enlarged version of the previously published book by this author, entitled "Tabellen zur Fourier Transformation" (Springer Verlag 1957). Then (a) is called the discrete Fourier transform (DFT) of (at). TABLE 5.1 Fourier Transform Properties Time Function Fourier Transform aF (W) + F2(W) Operation Linearity Time shift Time reversal afi(t) + bfz(t) f(t – to) f-t) F(we jest F(-) 0 Time scaling f(at) la -FC) ( Time transformation f(at - to) F(t) Duality Frequency shift Convolution 1 F e-jwto/a al a 21f(-w) F(w-wo) F (w)F2(0) f(t)ejant f(t)*f (t) Modulation (Multiplication) f(t)f (t) Fi(w)*F2() 27T Integration fludo f(T)dt i "(W) + F(0)8(w) Differentiation in time (jw)"F(W) d" dt" (-jt)"f(t) Differentiation in Frequency d" do" Symmetry f(t) real F(-w) = F"(w) The function F (j) is called the Fourier Transform of f (t), and f (t) is called the inverse Fourier Transform of F (j). Using the tables of Fourier Transform Pairs and Fourier Transform Properties, find the Fourier Transform of each of the following signals: a.


 0 kommentar(er)
0 kommentar(er)
